Alma mater, János Bolyai und die Geburt der nichteuklidischen Geometrien
János Bolyai und das Parallelen-Problem : Die Geburt der nichteuklidischen Geometrien
In diesem Vortrag - auch wenn er nicht direkt mit der Geschickte der Universität Gießen verbunden ist - möchte ich eine interessante Geschichte aus den Jahren um 1830 erzählen. Diese Geschichte gibt einen Einblick in das wissenschaftliche Leben dieser Zeit. Es liest sich wie ein moderner Kriminalroman und ist voll gespickt mit Genialität, Trauer, Dummheit und Ungerechtigkeit.
Die Geometrie war schon in der Antike einer der Grundpfeiler der Mathematik. Euklid war der erste Mathematiker der Antike, der eine vollständige Arbeit über die Grundlagen der Geometrie geschrieben hat, die „Elemente“. Euklid hat in seinem dreizehnbändigen Werk die Geometrie axiomatisch aufgebaut: Auf einigen wenigen grundlegenden Aussagen (Postulate, Definitionen und Axiomen) basierend, werden alle andere Gesetze der Geometrie abgeleitet. Jeder neuer Satz basiert nur auf diesen grundlegenden Aussagen und auf den anderen bereits bewiesenen Sätzen.
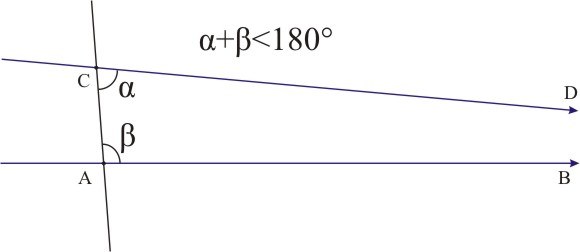
Eines dieser Postulate, das Parallelenpostulat, war irgendwie anders und hat von Anfang an die Mathematiker gestört. In den „Elementen“ des Euklid findet sich dieser Satz als das fünfte Postulat in folgender Formulierung: "…wenn eine Gerade AC beim Schnitt mit zwei Geraden AB und CD bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei rechte Winkel werden, dann die zwei geraden Linien AB und CD bei Verlängerung ins Unendliche sich treffen auf der Seite von AC, auf der die Winkel liegen, die zusammen kleiner als zwei Rechtecke sind."
 |
|
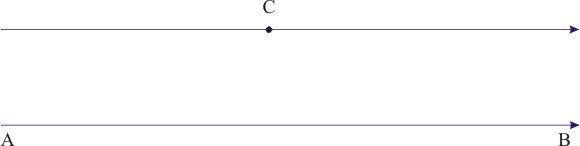
Die Geschichte der Parallellinien gehört zu den faszinierendsten Themen der Geistes-geschichte. Über 2200 Jahre hat das fünfte Postulat viele Mathematiker fasziniert, irritiert, herausgefordert und gequält. Noch in der Antike war den Mathematikern aufgefallen, dass dieses Postulat anders ist alle anderen. Dieses Postulat kann niemand selbst überprüfen, niemand kann unendlich lange Linien zeichnen. Darüber hinaus wurde seitdem vermutet, dass es mit Hilfe der anderen Postulate und Axiomen bewiesen werden kann, d.h. es ist gar kein Postulat. Viele Mathematiker haben es 2200 Jahre lang versucht dieses Postulat zu beweisen. Sehr viele haben sogar behauptet, einen Beweis gefunden zu haben. In allen solchen Fällen hat sich immer später herausgestellt, dass in den Beweisen ein Fehler steckt. Das einzige Ergebnis dieser Bemühungen sind die gleichwertigen Formulierungen dieses Postulats. Eine alternative Formulierung besagt, dass zu einer Geraden AB durch einen externen Punkt C nur eine einzige Parallele existiert. |
 |
|
Man kann sich genauso fragen, wie groß ist der Winkel ACD ist, wenn die Parallelen AB und CD durch eine zu AB senkrecht stehende Gerade CA geschnitten wird. |
 |
|
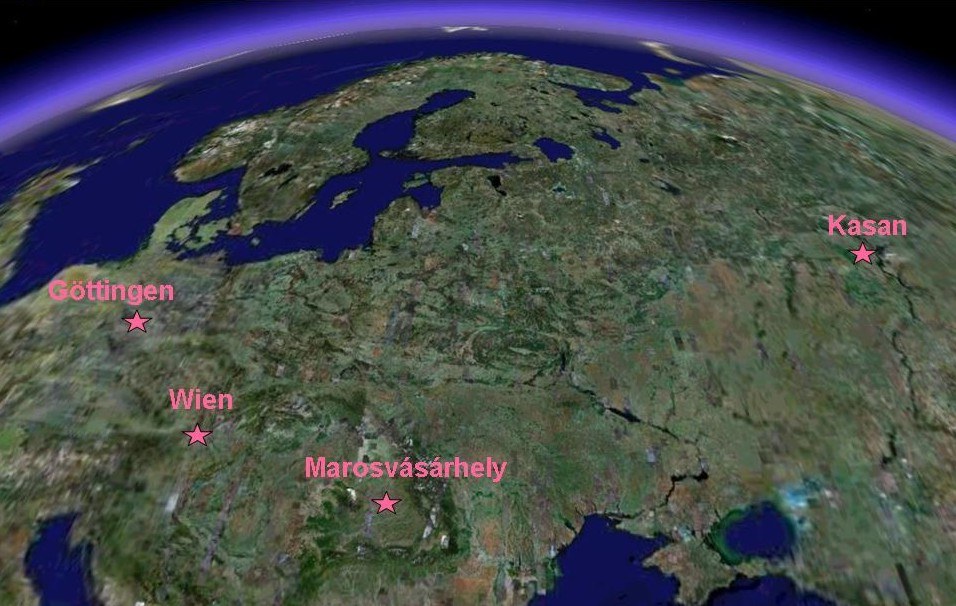
Dass es nicht 89° sind, kann jeder mit einem Winkelmesser nachprüfen. Die Frage ist ob es eventuell nicht 89.999999999999999999999999999° ist. Dass dieser Winkel 90.0° ist, wird in der Euklidischen Geometrie postuliert. Diese Aussage scheint nicht nur selbstverständlich zu sein, denn seit Maimonides gilt sogar die These: „Die Wahrheiten der Geometrie liegen über Gott“. Kant betrachtet den Raum mit seiner euklidischen Geometrie auch als a priori gegeben. Der Mathematiker Bolyai János war der Erste, der das menschliche Denken um 1830 von diesem verwurzelten Vorurteil befreit hat. Er hat unseren Weg zu einem ganz neuen Verständnis des Raumes geebnet. Seine Lebensgeschichte möchte ich nun erzählen. Die Schauplätze dieser Geschichte sind die Städte Marosvásárhely (Siebenbürgen, Kaisertum Österreich), Kasan (an der Wolga, Russland) und Göttingen. |
 |
|
Der berühmte deutsche Mathematiker Carl Friedrich Gauss (geb.1777, Braunschweig) und der ungarische Mathematiker Bolyai Farkas (geb.1775, Bólya in der Nähe von Hermannstadt, Siebenbürgen) haben von 1796 bis 1799 zusammen in Göttingen studiert und sich angefreundet. Gauss wurde Mathematikprofessor an der Universität Göttingen, Bolyai an der evang.-reform. Kollegium zu Marosvásárhely. |
 |
|
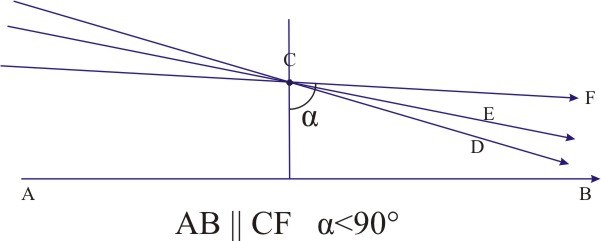
Bolyai János, Sohn von Bolyai Farkas, wurde 1802 in Klausenburg (Siebenbürgen) geboren und war schon als Kind ein mathematisches Genie. Mit 14 studierte er schon höhere Mathematik. Nach dem Absolvieren des Kollegiums ist der Vater mit dem Problem konfrontiert einen geeigneten Studienplatz für seinen hochbegabten Sohn zu finden. An den Universitäten von Wien und Budapest gab es damals keinen Mathematikprofessor, bei dem der Junge etwas hätte lernen können. Bolyai hat bei Gauss nachgefragt, ob sein Sohn bei ihm in Göttingen studieren könnte, seine Anfrage blieb unbeantwortet. Aus finanziellen Gründen kann Bolyai János nur an der Militäringenieur-akademie in Wien studieren. Bolyai János war früh mit dem Problem der Parallelen konfrontiert, da sein Vater versucht hatte das Parallelenaxiom zu beweisen. Zu seinem Sohn sagte er öfters: „Wer das Parallelenaxiom beweisen kann, verdient einen Diamanten so groß wie die Erde“. Ab 1818 beschäftigt sich Bolyai János mit dem Wesen des Parallelenaxioms. Sein Vater hatte versucht, ihn auf jede erdenkliche Weise davon abzubringen, um nicht Zeit und Kraft mit unfruchtbaren Untersuchungen zu vergeuden. Bolyai János beendete 1823 sein Studium, er hatte inzwischen eine neue Theorie der Parallelen ausgearbeitet. Er schrieb seinem Vater (aus Temeswar): „Ich habe aus Nichts eine neue Welt geschaffen.“. 1826 übergibt er seinem ehemaligen Lehrer an der Militär-ingenieurakademie die deutschsprachige Arbeit über die nichteuklidische Geometrie. 1831 erscheint sein Werk auf Latein, der „Scientiam spatii“ (Appendix), die Lösung des 2200 alten Parallelenproblems: Es gibt gar kein Problem, es existiert eine euklidische und eine nichteuklidische Geometrie. Die nichteuklidische Geometrie unterscheidet sich von der euklidischen Geometrie dadurch, dass hier das Parallelenaxiom nicht gilt, da verschiedene Geometrien von verschiedenen Axiomen ausgehen. In der nichteuklidischen Geometrie gilt, dass es durch einen Punkt außerhalb einer Geraden nicht exakt eine Parallele gibt. Wie werden zwei Geraden parallel? Nach Bolyai können wir uns das folgenderweise vorstellen: Seien AB und CD zwei Geraden, die sich schneiden. Wenn man die Gerade CD um den Punkt C rotiert, „springt“ diese Gerade irgendwann in die Position CF, in der sich die Geraden AB und CF nicht mehr schneiden. In dieser Position sind die Geraden AB und CF parallel. |
 |
|
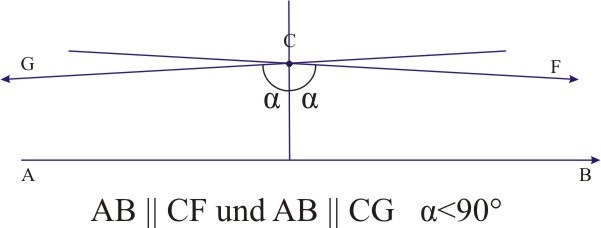
Bolyai hat angenommen, dass der Winkel α nicht 90° ist und hat, ausgehend von dieser Tatsache, eine ganz neue Geometrie („neue Welt“) aufgebaut, in der das Parallelenaxiom nicht mehr gültig ist. Er nennt sie die „absolut wahre Geometrie des Raumes“. In einer solchen Geometrie kann man z. B. durch ein Punkt C zwei Parallelen zu einer Geraden AB zeichnen. |
 |
1832 liest Gauss das Appendix und schreibt im Februar an dem Marburger Professor Gerling: „Ich halte diesen jungen Geometer v. Bolyai für ein Genie erster Grösse“. Aber im März 1832 behauptet er in seinem Brief an Bolyai Farkas die ganze Arbeit von Bolyai János schon längst gewusst zu haben:„Wenn ich damit anfange <<dass ich solche nicht loben darf>>: so wirst Du wohl einen Augenblick stutzen: aber ich kann nicht anders; sie loben hiesse mich selbst loben: denn der ganze Inhalt der Schrift, der Weg, den Dein Sohn eingeschlagen hat, und die Resultate zu denen er geführt ist, kommen fast durchgehends mit meinen eigenen, zum Theile schon seit 30-35 Jahren angestellten Meditationen überein. In der That bin ich dadurch auf Äuserste überrascht“. Gauss bleibt merkwürdigerweise stumm und verschweigt die Arbeit vor der mathematischen Gemeinde. Dadurch zerstört er jede Hoffnung von Bolyai János eine angemessene Würdigung seiner eigentlichen großen mathematischen Leistung noch zu Lebzeiten zu bekommen.
1829 schreibt der russische Mathematiker Nikolai I. Lobatschewski (Kasan) einen Artikel über die nichteuklidische Geometrie in einer universitätseigenen Zeitschrift auf Russisch. Lobatschewski entwickelt anschließend auch die Theorie der nichteuklidischen Geometrie (ohne über die Arbeiten von Bolyai gewusst zu haben) die er 1840 auf Deutsch drucken ließ. Gauss liest 1840 auch diese Arbeit, jedoch lobt er sie merkwürdigerweise dieses Mal (aber auch nur in einem Brief). Er lässt Lobatschewski als korrespondierendes Mitglied der „Akademie der Wissenschaften zu Göttingen“ wählen. Gauss informiert Lobatschewski nicht über die Arbeit von Bolyai János.
Bolyai János und Nikolai I. Lobatschewski haben eine angemessene Würdigung ihrer großen mathematischen Leistung nicht mehr erlebt. Zu revolutionär, zu unverständlich und außer-gewöhnlich waren ihre Überlegungen. Die meisten Zeitgenossen haben die dem gesunden Menschenverstand völlig zuwiderlaufende Konstruktion einer euklidischen Geometrie jenseits des Parallelenaxioms nicht verstanden.
Die Gedanken von Bolyai János zu den Grundlagenfragen der Geometrie führten zu einer vielschichtigen Entwicklung. Sie wirkten sich auf Ausgangspunkte des Aufbaus der Mathe-matik aus und fanden Anwendung in vielen Teilen der Physik und in der Astronomie.
Bis vor kurzem haben die Astrophysiker gedacht, dass die Geometrie des Universums eine Geometrie mit einer konstanten negativen Krümmung ist, wie von Bolyai János beschrieben. Die Auswertung der Raumrichtungsabhängigkeit der kosmischen Mikrowellenhintergrund-strahlung hat gezeigt, dass unser Universum mit hoher Wahrscheinlichkeit tatsächlich eine euklidische Raumstruktur hat.
